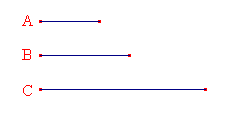
命題16
もし、2つの数が互いに素ならば、そのとき、第1が第2に対するように、第2は他のどのような数にも対さない。

2つの数が互いに素であるとせよ。
AがBに対するように、Bは他のどのような数にも対さないと主張する。
もし可能ならばAがBに対するように、BをCに対するとせよ。
AとBは素で、素数は最小で、最小の数は同じ比をもつ数を割り切り、商は同じで、前項は前項を割り切り、後項は後項を割り切る。propositionⅦ21
それゆえに、前項は前項を、つまり、AはBを割り切る。propositionⅦ20
しかし、Aはそれ自身を割り切る。
それゆえに、Aは互いに素であるAとBを割り切り、これは不可能である。
それゆえに、もし、2つの数が互いに素ならば、そのとき、第1が第2に対するように、第2は他のどのような数にも対さない。